A-C-I: Assessment, Curriculum, Instruction

Project resources and activities are designed to make explicit connections between content topics and curriculum needs, assessment practices and resources, and instructional strategies. While the connection between and among assessment, curriculum and instruction are often referred to as CAI, we have chosen to refer to this connection as ACI to stress the importance of the formative and ongoing role of assessment in the process. Listing the A for assessment prior to the C (curriculum) and I (instruction) makes explicit the need to pre-assess students before determining the program of learning and selection of activities. While the content to be learned is central to the plan, the assessment will drive the instruction and inform any subsequent activities related to that process. Assessment in this model is formative and ongoing. The open educational resources are meant to assist and support the learning process.

TPACK Framework

(Source: http://tpack.org/)
D

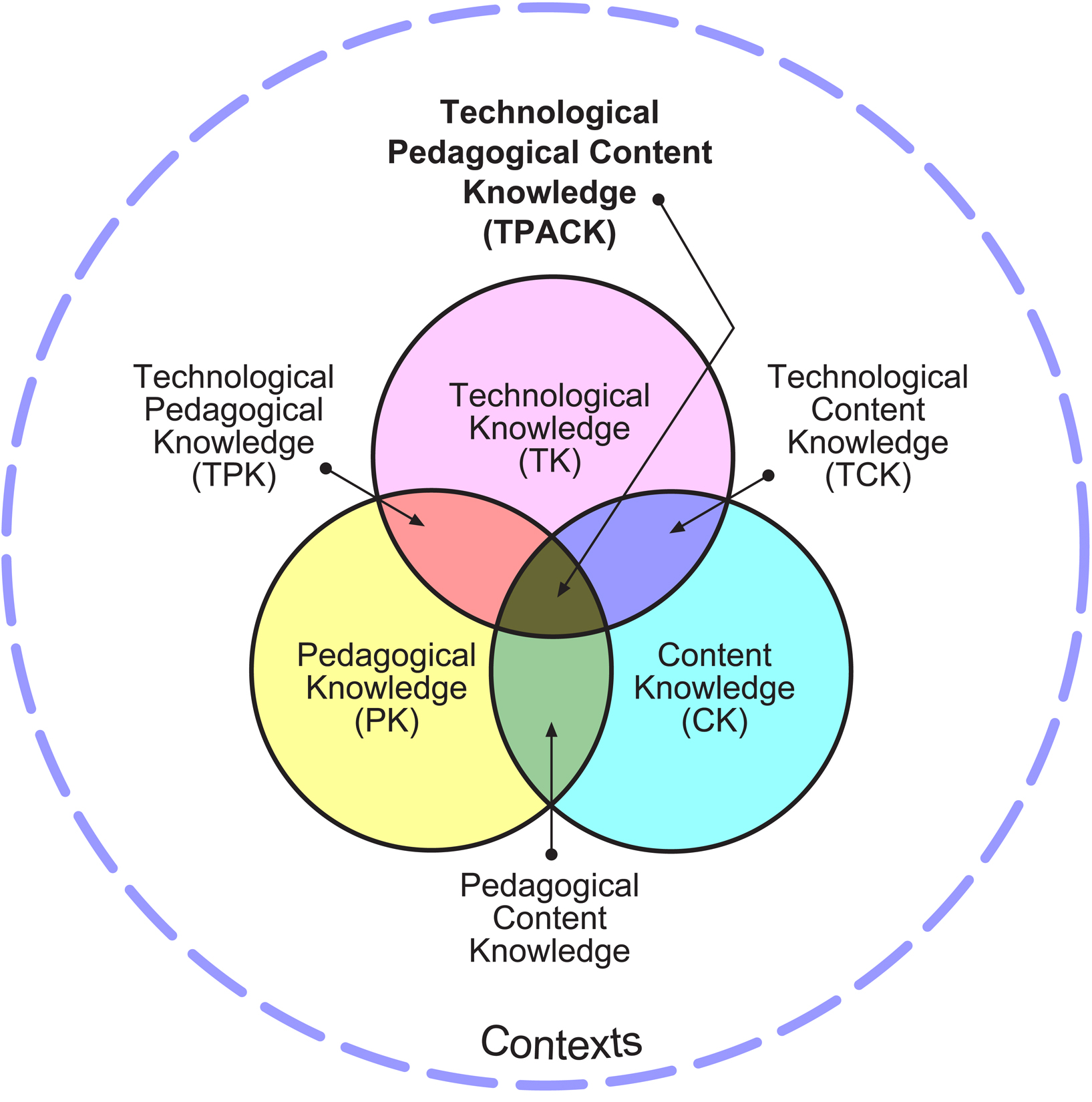
Teaching mathematics well demands proficiency across a variety of domains and draws on a variety of resources and strategies. One way to make sense of these multiple domains within the context of integrating technology in learning and teaching is to use the technological pedagogical content knowledge (TPACK) framework, which separates the primary domains of teaching into (T) technological, (P) pedagogical, and (CK) content knowledge. This construct builds on the ideas of Lee Shulman (1986), who described pedagogical content knowledge (PCK) as more than just generalized pedagogical knowledge and subject-specific content knowledge. Teacher's PCK was described as what is needed to help learners gain subject-specific content knowledge. PCK includes, for example, the most powerful representations of topics for building conceptual understanding, the most common student misconceptions or stumbling blocks, and understandings about what makes specific topics easy or difficult for learners (Shulman, p. 9).

Similarly, within the context of integrating technology in learning experiences, the TPACK framework situates technological knowledge as a third primary domain and defines the technological knowledge needed for teaching to be different from generalized technological knowledge or even knowledge of how to use appropriate technologies within a specific content area; pedagogical knowledge specific to the technology and content is needed. For example, a mathematics teacher who has gained proficiency using a graphing calculator for personal tasks may not know how to effectively integrate graphing calculators in learning experiences for students building specific concepts and skills. A visual model of the TPACK framework shows the seven areas of knowledge defined by the framework. The model illustrates the complex intersections of knowledge areas and also helps reinforce effective teaching with technology as the intersection of the three domains. These intersecting domains will be evident throughout the OER in Mathematics Professional Development Project and will be clarified and made more explicit through multiple media including video, audio, screen casts, discussions and interactive examples. The tools and resources developed within the project will be free and open for use in the classroom.

To learn more about the TPACK framework for mathematics teaching refer to the article Mathematics Teacher TPACK Standards and Development Model  (.pdf file) (Niess, et al., 2009).

References

Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper S. R., Johnston, C., Browning, C., Özgün-Koca, S. A., & Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education, 9(1), 4-24.

Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher. 15(2), 4-14.